Exploring JavaScript Features of Functional Programming

In this blog post I decided to dig into some functional programming features in JavaScript.

As the name may imply, functions are at the center of Functional Programming (FP), but the main concept in FP is how we use functions.

What do I mean by "how we use functions"?

Well, for that, we should first understand functions inside and out.

What is a function?

In math, a function is like a machine that takes an input and returns an output, while the output is related to the input.

You probably remember from math class in school the equation:

y = f(x)

Now let's have a look at the following equation:

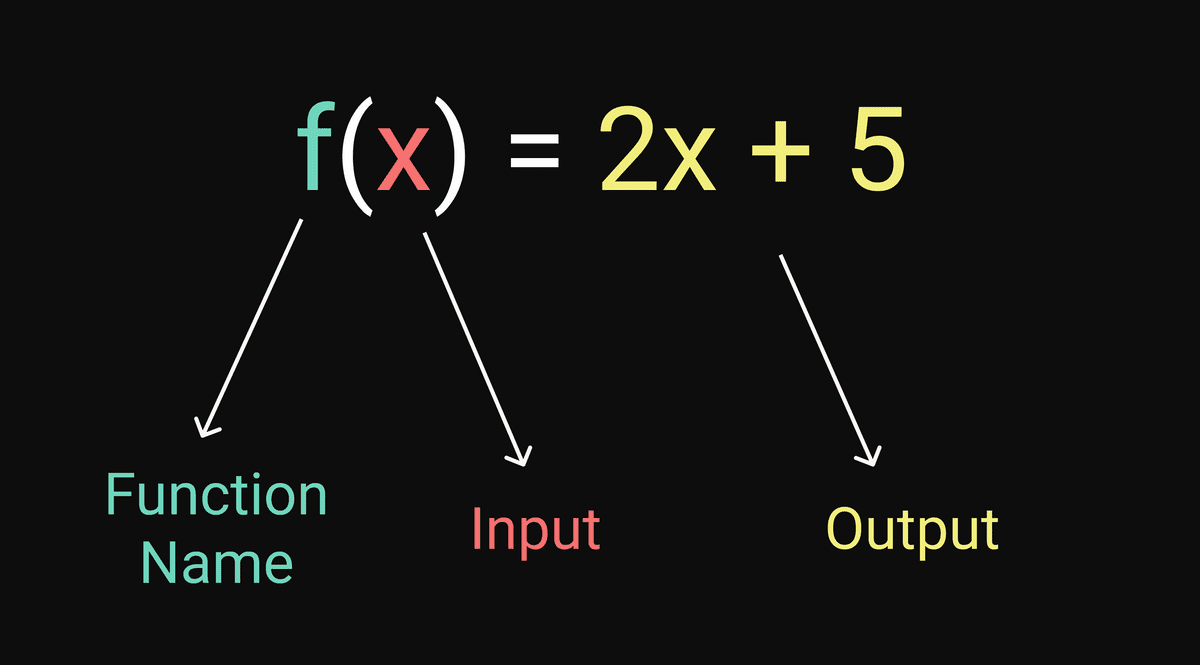
Given the above example X = 2, what would be the value of y?

Correct! 9

What does it mean and what does any of this got to do with FP? 🤨

For the given function, with X = 2, we can interpret the input and the output values as a point in a Cartesian Coordinate System (2, 9), and we can say that:

f(2) = 9

To use the function in other equations, you can write f(2), which has the same meaning as 9. In other words, you can think of math function as mapping from input to output.

Now, let's have a look at the following function expression:

const multiplyAndAdd5 = x => x * 2 + 5;

Say X = 2, that will give us:

multiplyAndAdd5 = 9

In JavaScript, the value of a function expression is the function itself, meaning that call multiplyAndAdd5 without invocation (parentheses), would give us:

[Function: multiplyAndAdd5]

If you want to get the returned value of a function, you must invoke it with a function call (parentheses), and apply arguments.

const multiplyAndAdd5 = x => x * 2 + 5;
multiplyAndAdd5(2); // 9

Like in the math example, where f(2) can be replaced with 9, here, we can replace multiplyAndAdd5(2) with 9.

In FP, this term called 'morphism'. Morphism means that a set of values can be mapped to another set of values.

In the beginning of this article, I have mentioned that the input(s) (a set of values) of a function is related to the output of that function (mapped to another set of values). That is morphism (mapping) and how functions in math are related to functional programming.

What is this 'input' all about?

Many programmers are confused between parameters and arguments.

Parameters are the named variables inside the function (x and y).

Arguments are the values you pass to the function when you call it (4 and 1).

function foo(x, y) {
  // ...
}
foo(4, 1);

There are different ways to pass parameters to a function:

1. Default Parameters

In ES6 we can initialize parameters with a value. In that case, if we don't pass an argument when we call the function, or we pass undefined, the default assignment expression will substitute. If we pass an argument, it overrides the default params value.

function foo1(x, y = 4) {
  return x + y;
}
foo1(1); // 5
function foo2(x, y = 4) {
  return x + y;
}
foo2(7, 1); // 8

ES6 - Default Parameters

2. Named Arguments

In ES6 we can use destructuring and pass object literals as arguments to a function. Be aware that now, I am referring to how we invoke the function, therefore I have mentioned arguments and not parameters.

ES6 - Destructuring

Named arguments can assign default values to parameters using the default parameters feature.

const createUser = ({
    name,
    avatar,
    nickName = 'tempNickName'
}) => ({
    name,
    avatar,
    nickName
});
const Tom = createUser({
    name: 'Tom',
    avatar: 'avatars/tom.png',
    nickName: 'TomTheCat'
});
Tom; // {name: 'Tom', avatar: 'avatars/tom.png', nickName: 'TomTheCat'}

With named arguments, the function doesn't depend on the order in which the arguments are passed. We can even skip the arguments we don't want to provide.

In contrast, functions can also take positional arguments. In this case, the caller has to make sure that the 'name' is the first argument, and the 'nickname' is the second argument.

Using positional arguments is usually fine for cases where you pass one or two arguments, but if you have some util function which takes 4 or more arguments, it would be hard to remember the order of arguments to pass.

You don't want to pass email in place of the password argument.

const loginUser = (name, email, password) => {
  // ... login operation that we don't care about :) ...
  return `Hi ${name}`;
}
const loggedInUser = loginUser('Nicholas', 'nic@mailo.com', '123rememberME');

Using positional arguments introduces some challenges:

• We cannot skip the arguments in the middle
• Adding types (in TypeScript) is less clean
• It might create subtle bugs

3. Rest, Spread and ...args

Rest - gathers individual elements together into an array.

Rest Parameters

const multiply = (multiplier, ...theArgs) => {
  return theArgs.map(element => {
    return multiplier * element;
  })
}
const multipliedArr = multiply(2, 15, 25, 42);
console.log(multipliedArr)  // [30, 50, 84]

In the above example, we passed '2' as the first argument, which is the 'multiplier', and the rest arguments are '...theArgs'.

Spread - spreads the elements from an array to individual elements. Can be used also in object literals.

Spread Syntax

const sum = (a, b, c, d) => a + b + c + d;
const numbers = [2, 5, 7, 6];
sum(...numbers) // 20

The 'sum' function doesn't expect to get an array, we pass to it individual elements by spreading the 'numbers' array.

...args (and arguments) - each function has an arguments object (except arrow functions) that holds a reference to each of the arguments passed in.

The Arguments Object

'Arguments' is array-like, meaning that it has a length property, but it doesn't have Array's built-in methods. But be careful and never access arguments positionally, like arguments[1].

function myVeryUsefulFunc(a, b, c) {
  console.log(arguments.length);
}
myVeryUsefulFunc(1,2); // 2

If, for any reason, you need to access a specific index, you can use the rest operator with 'args'. args will always be an array, but it will not include values that are assigned to the a, b, and c parameters, only anything else that’s passed beyond those first three values.

function myVeryUsefulFunc(a, b, c, ...args) {
  console.log(a, b, c, ...args );
}
myVeryUsefulFunc(1, 2, 3, 4, 5, 6, 7); // 1, 2, 3, [4, 5, 6, 7]

4. Function

No, this is not a mistake, we are still in the input section and this one is about functions that take another function as an input. In the professional, fancy FP jargon those functions are called higher order function.

A higher order function is a function that takes another function as an argument or returns another function.

In order to wrap our head around what it means and what all this long introduction is about, let's take our good old multiplyAndAdd5 from the beginning.

const multiplyAndAdd5 = x => x * 2 + 5;
const numbers = [1, 2, 3, 4];
numbers.map(multiplyAndAdd5); // 7, 9, 11, 13

It is kind of hidden from us, but Array.map(), Array.filter(), Array.reduce(), Array.forEach(), etc... all of them are higher order function - they receive a function (callback) as an argument.

In our example, the callback function we pass to numbers.map() is multiplyAndAdd5. This callback function takes 3 arguments (no parameters because I'm referring to the invocation, i.e. when we call the function): the first is the current item in the array, the second is the index of that item, and the third is the entire array ('numbers').

What is this 'output' all about?

In FP, our functions should always have output - a returned value.

The returned value could be any data type: array, object, string, number, boolean, and even function (higher order functions), but it can't be undefined. It also must be a single value, therefore, if your function needs to return multiple values, you should return an array or object with those values.

The return statement doesn't just return a value from a function, it is also ends the execution of the function.

Going back a few sentences ago, I have mentioned higher order function, and that they can not only take a function as an argument, but also can return a function. This leads us, finally, to the blog's post title, but before... 😏

Let's sum up this section so far. These input and output that we have seen are a part of something called function signature, and it consists of:

1. Function name (optional)
2. Input(s) - parameters (may optionally be named)
3. Output - the type of the returned value (in TypeScript, Javascript engine will figure out the types at runtime)

Currying

A curried function is a function that takes multiple parameters, one at a time (this is the key takeaway, so remember it). Given a function with 3 parameters, it takes a parameter, and returns a function that takes the next parameter, and so on until all parameters have been supplied, and the final value is returned.

• Arrow function style

const add = a => b => c => a + b + c;

• Function keyword style

function add(a) {
  return function(b) {
    return function(c) {
      return a + b + c;
    }
  }
}

Take a look at the function keyword style example.

What is the first thing that you see?

Yep, it's a closure.

A closure is a function that remembers and accesses variables from outside of its own scope, even when that function is executed in a different scope.

function c() has access to variables 'a' and 'b', therefore, we can make the calculation without getting an error.

(more about closures in one of my previous posts closures).

Another thing we can learn from this function if that the add() function takes one argument, and then returns a partial application of itself with a fixed in the closure scope.

Partial Application

A partial application is a function which has some arguments fixed inside its closure scope.

what's the difference between curry and partial application?

1. Partial application can take as many as arguments a time as desired. Curried function always return unary function (a function that takes one argument).
2. All curried functions return partial applications, but not all partial applications are the result of curried functions.

Function Composition

Function composition is the process of passing the return value of one function as an argument to another function.

Going back to math for a while:

f: a => b
g: b => c

We can create a new function from a composition between f and g:

h: f * g
h: a => c
h(x) = f(g(x))

Translating to JavaScript:

const f = n => n + 2;
const g = n => n * 2;
const h = x => f(g(x));
h(10); // 22

Just like in math, where we calculate first what's in the inner braces, the code above is evaluated from the inside out:

1. x is evaluated
2. g() is applied to x
3. f() is applied to the return value of g(x)

We saw that h: f * g and h(x) = f(g(x)) so it's equivalent to:

(f * g )(x) = f(g(x))

Which can be translated to JavaScript:

const compose = (f, g) => x => f(g(x));

Compose() creates a pipeline of functions with the output of one function connected to the input of the next function.

Combined Curry and Function Composition

Curried functions are particularly useful in the context of function composition.

Something that really helped me to understand it more was to implement compose() with reduce, or more precisely - Array.reduceRight()

const compose = (...fns) => x => fns.reduceRight((g, f) => f(g), x);

And the opposite, which is pipe(), implementing with Array.reduce():

const pipe = (...fns) => x => fns.reduce((g, f) => f(g), x);

In both implementations, we use the rest operator in order to extract the functions and then take one parameter (function) at a time and compose them together.

Function composition creates very concise, readable code, but it comes with the cost of debugging.

Say we want to inspect the values between functions, we can write 'trace()' utility function that implements a form of curried function and helps us log our values.

const trace = label => value => {
  console.log(`${ label }: ${ value }`);
  return value;
}

Now let's use 'trace()' on one of our previous examples and the 'pipe()' implementation:

const pipe = (...fns) => x => fns.reduce((g, f) => f(g), x);
const f = n => n + 2;
const g = n => n * 2;
const traceAfterF = trace('trace after f');
const traceAfterG = trace('trace after g');
const h = pipe(g, traceAfterG, f, traceAfterF);
h(10);
// trace after g: 20
// trace after f: 22
// 22

Each time we call trace() with a label, we get a specialized version of the trace function that is used in the pipeline, where the label is fixed inside the returned partial application of trace().

Abstraction

Abstraction is the process of considering something independently of its associations, attributes and "hides" unnecessary information.

The most useful implementation of abstraction is pure functions. A pure function is a function which given the same input, will always return the same output.

Abstraction also helps us to write less code while doing actually more.

function saveComment(txt) {
    if (txt !== "") {
        comments[comments.length] = txt;
    }
}
function trackEvent(evt) {
    if (evt.name !== undefined) {
        events[evt.name] = evt;
    }
}

In the above example, both functions kind of do the same thing. Therefore, we can use abstraction in function storeData() with parameters and call it when needed with the suitable arguments.

function storeData(store, location, value) {
    store[location] = value;
}
function saveComment(txt) {
    if (txt !== '') {
        storeData(comments, comments.length, txt);
    }
}
function trackEvent(evt) {
    if (evt.name !== undefined) {
        storeData(events, evt.name, evt);
    }
}

Connecting this concept of abstraction with currying and partial application, by looking (again) at Array.map(): 'map' is a higher-order function that abstracts away the idea of applying a function to each element of an array in order to return a new array of processed values.

const curriedMap = fn => arr => arr.map(fn);
const calcTax = taxValue => salary => taxValue/100 * salary;
const calcTaxAll = curriedMap(calcTax(5));
const taxValToSubtractFromSalaries = calcTaxAll([17_000, 12_000, 17_000, 25_000]);
taxValToSubtractFromSalaries; // [850, 600, 850, 1250]

The curriedMap() takes the specializing function and then returns a specialized version of itself that takes the array to be processed. We now can use curriedMap() and calcTaxAll() with any 'taxValue' and any array of salaries.

Conclusions

In functional programming, it's all about functions, and it takes advantage of functions in math. We have input(s) and an output, and the output is connected to the input. Our inputs can be in different forms, structures, and even can be seperated, so they can be passed one at a time. All of that helps us to write composable functions and make our code more abstract, concise, readable and easy to reason about.

Thanks for reading. Hope I managed to explain these concepts clearly and that you have learned something new, or at least understand these concepts more than before.

If you think I'm a cool person, and you want to work with me and even find bugs in my code 🪲

We are hiring QA and Automation Manager

You can contact me via one of the media options down below.

Resources:

1. Functional Light Javascript by Kyle Simpson
2. Composing Software by Eric Eliot